A quantum computer is a device that performs computation by controlling and measuring quantum states. Quantum computers were first proposed in the 1980s by several physicists, notably Paul Benioff, David Deutsch, Richard Feynman, and Yuri Manin. It is widely believed that quantum computers should be capable of performing computations that would not be feasible on a classical computer, particulary problems in computational chemistry which require the simulation of quantum states. Effective quantum computing would also jeopardize the cryptographic protocols that are used to secure Internet communication.
It is only in recent years that quantum computers have been available for use by the general public. The technology is emerging but immature—there are no known commercial uses for currently existing devices. There are significant challenges in creating a useful quantum computer, the greatest being error correction.
A quantum computation has three stages:
- Prepare a quantum state. This may require encoding the input as a quantum state, or initializing to a known state.
- Apply a unitary operator to the state. The unitary operator is defined by a quantum circuit.
- Perform a measurement of the result.
Quantum computation uses a particular type of quantum state, called a quantum register.
Qubits
We recall that a classical bit has one of two distinct states, usually denoted 0 and 1.
The state of a quantum bit, hereafter called a qubit, is a vector quantity. There are two basic states for a qubit, denoted $|0\rangle$ and $|1\rangle$.
$$|0\rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \qquad |1\rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix}.$$
In general, the state of a qubit $|\psi\rangle$ is a linear combination of the basic states $|0\rangle$ and $|1\rangle$.
$$|\psi\rangle = a |0\rangle + b |1\rangle = \begin{pmatrix} a \\ b \end{pmatrix}.$$
The coefficients $a$ and $b$ are complex numbers, and they are required to satisfy $|a|^2 + |b|^2 = 1$. This implies that the state of a qubit is always a unit vector, i.e. it has length 1.
It is not possible to observe the values of $a$ and $b$ directly. When the quantum state $|\psi\rangle$ is measured, the result is either 0 or 1, with probabilities $|a|^2$ and $|b|^2$ respectively. Subsequent measurements of this state will always yield the same result.
Quantum registers
A quantum register is composed of several qubits. An $n$-qubit register has $2^n$ basic states, which are labeled with bitstrings. For example, a 2-qubit register has 4 basic states:
$$
|00\rangle = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix},\quad
|01\rangle = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix},\quad
|10\rangle = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix},\quad
|11\rangle = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}.$$
Likewise, a 3-qubit register has 8 basic states (we will omit the column vectors):
$$|000\rangle, |001\rangle, |010\rangle, |011\rangle, |100\rangle, |101\rangle, |110\rangle, |111\rangle.$$
If we interpret the bitstrings as binary numbers then we can write the basic states as
$$|0\rangle, \ |1\rangle, \ |2\rangle, \ |3\rangle, \ |4\rangle, \ |5\rangle, \ |6\rangle, \ |7\rangle.$$
In general, the state of an $n$-qubit quantum register is a linear combination of the $2^n$ basic states, with complex coefficients (called amplitudes). The squared absolute values of the amplitudes always sum to 1, and they represent the probabilities of measuring the quantum register in each of the $2^n$ basic states.
For example, if $$|\psi\rangle = 0.7 |0\rangle + (0.3 - 0.4 i) |1\rangle - 0.5 |2\rangle + 0.1 i |3\rangle$$ then the measurement of $|\psi\rangle$ has four possible results:
- 0 with probability $|0.7|^2 = 0.49$,
- 1 with probability $|0.3 - 0.4 i|^2 = 0.25$,
- 2 with probability $|-0.5|^2 = 0.25$, or
- 3 with probability $|0.1 i|^2 = 0.01$.
We can express the state $|\psi\rangle$ of an $n$-qubit quantum register concisely as
$$|\psi\rangle = \sum_{k=0}^{2^n-1} \lambda_k |k\rangle$$
where $\lambda_k \in \mathbb{C}$ and $\sum_{k=0}^{2^n-1} |\lambda_k|^2 = 1$.
When the state $|\psi\rangle$ is measured, the result is $k$ with probability $|\lambda_k|^2$.
Inner products
The inner product of two complex vectors
$$|v\rangle = \begin{pmatrix}v_0 \\ v_1 \\ v_2 \\ \vdots \\ v_{N-1} \end{pmatrix} \text{ and } |w\rangle = \begin{pmatrix}w_0 \\ w_1 \\ w_2 \\ \vdots \\ w_{N-1} \end{pmatrix}$$
is defined by
$$\langle v|w\rangle = \sum_{k=0}^{N-1} v_k^* w_k,$$
where $v_k^*$ denotes the complex conjugate of $v_k$. If $v_k = a + bi$ then $v_k^* = a - bi$.
Two vectors are said to be orthogonal (or perpendicular) if the inner product between them is zero.
The length of a vector $|v\rangle$ is $\|v\| = \sqrt{\langle v|v\rangle}$. The length of a nonzero vector is always a positive real number.
Unitary operators
A unitary operator is a linear transformation from a complex vector space to itself that preserves inner products, and hence also preserves lengths. A unitary operator can be represented as a unitary matrix—a square matrix whose column vectors have length 1 and are orthogonal to one another.
Unitary operators are always invertible. The inverse of a unitary matrix is equal to its conjugate transpose.
The importance of unitary operators in quantum computing stems from the fact that every quantum circuit can be described as a unitary operator.
Quantum circuits and gates
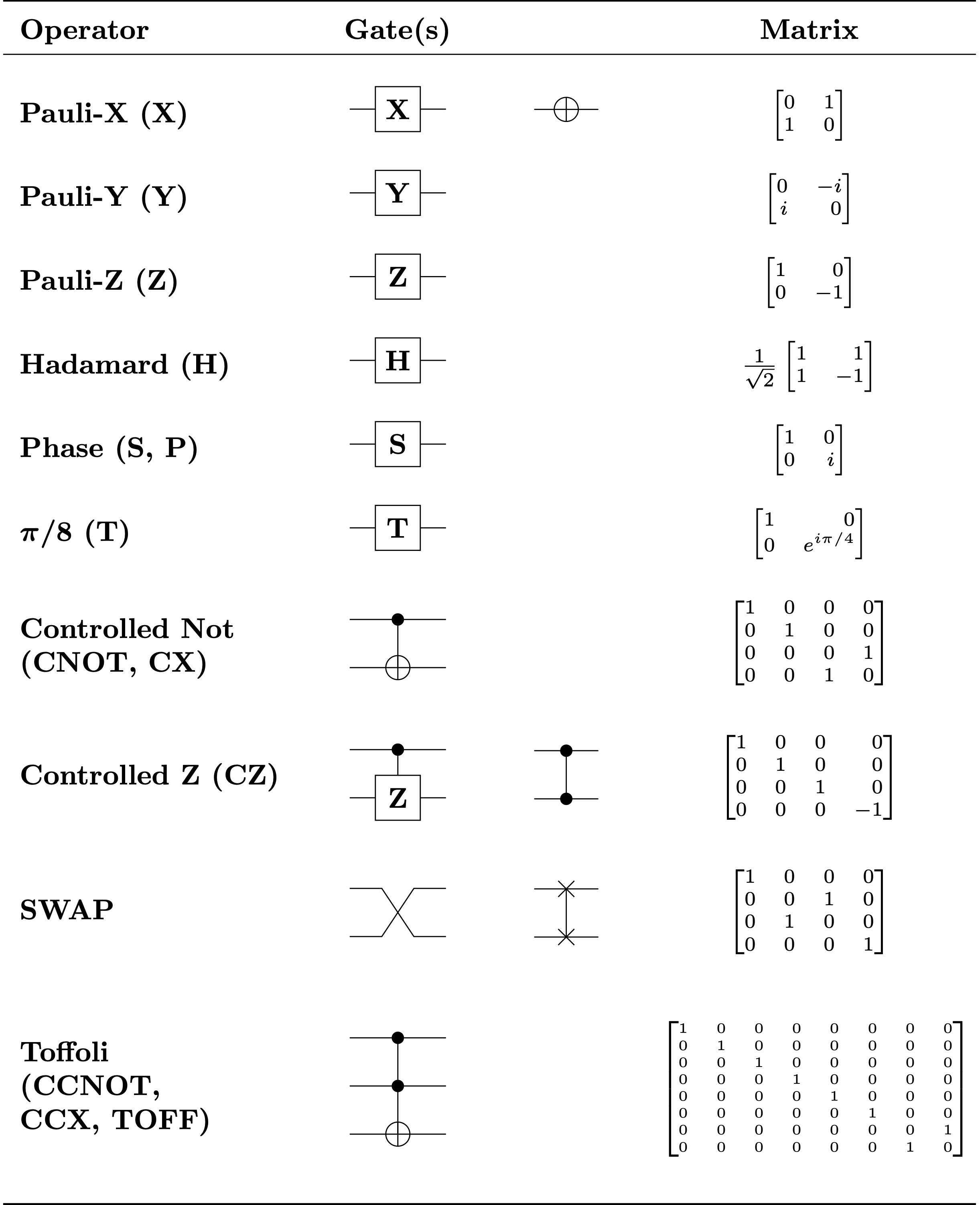
In a quantum computer, a unitary operator is realized by a quantum circuit, which is composed of quantum gates. Each quantum gate represents a unitary transformation, but it only acts on a few qubits at a time, usually 1 or 2. In effect, a quantum circuit is a matrix factorization of a large unitary matrix into smaller matrices. Some of the most common quantum gates and their matrices are shown in the table below.
Measurement
Measurement occurs at the end of a quantum computation. Since measuring a state can change the state, it is an inherently destructive process.
When a quantum state $|\psi\rangle = \sum_{k=0}^{2^n-1} \lambda_k |k\rangle$ is measured, one obtains an integer between 0 and $2^n - 1$, or equivalently, a bitstring of length $n$. The probability of obtaining $k$ is equal to $|\lambda_k|^2$. After the value $k$ is observed, the quantum state collapses to $|k\rangle$, and future measurements will always produce the same value $k$.
It is also possible to perform a partial measurement on some of the qubits. This results in one classical bit for each qubit that was measured. To find the probability of a given result, we discard the terms that are inconsistent with the observed result, then add up the squares of the absolute values of the remaining amplitudes. To find the new state after measurement, we normalize the remaining terms to have length one. This process is analogous to marginalizing a probability distribution.
Example: Suppose that the state is
$$|\psi\rangle = \lambda_0 |00\rangle + \lambda_1 |01\rangle + \lambda_2 |10\rangle + \lambda_3 |11\rangle.$$
If we measure the first qubit, then the result will be 0 with probability $p_0 = |\lambda_0|^2 + |\lambda_1|^2$, or 1 with probability $p_1 = |\lambda_2|^2 + |\lambda_3|^2$.
If the result is 0, then the new state is $\frac{\lambda_0}{\sqrt{p_0}} |00\rangle + \frac{\lambda_1}{\sqrt{p_0}} |01\rangle$.
If the result is 1, then the new state is $\frac{\lambda_2}{\sqrt{p_1}} |10\rangle + \frac{\lambda_3}{\sqrt{p_1}} |11\rangle$.
Variational circuits
Some problems require a combination of quantum and classical computing. Quantum deep learning uses variational quantum circuits. These are quantum circuits that have parameterized gates. The parameters are analogous to the weights in a deep neural network. The variational quantum circuit serves as a subroutine that is invoked by a classical computer, and backpropagation is used to estimate the optimal parameter values.
